The Marching Cubes Algorithm 1: Introduction & Procedural Cave Generation in 2D
The marching cubes algorithm
Introduction
During the holydays, since ETH wasn’t giving me enough work to do, I decided to learn how to use Unity. While deciding the project to implement, I stumbled upon the marching cube algorithms, so now here we are!
The problem
The main need the Marching Cube Algorithm tries to satisfy, is the need to form a facet approximation to an isosurface through a scalar field, sampled on a rectangle grid. A lot of big words huh? Let’s make this simple: imagine to have a lot of points nicely distributed on a section of space. We now decide which of these points we want to be contained in our 3d surface, and which not. There we are! We can now pass our “marching cube” over all the points and make it draw triangles to “exclude” external vertices: each triangle will have his vertices between an excluded cube vertex and an included one (see Figure 1 for a reference).
The algorithm
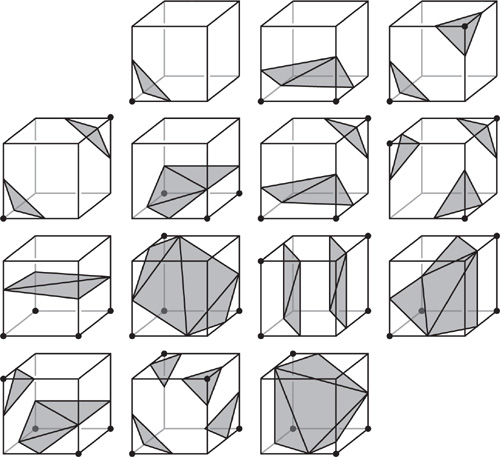
The main problem of this algorithm is the amount of data we’d need to compute, but luckily someone has already done that for us, and pre-computed tables are available online. As everyone knows a cube has 8 vertices. Since each one of those vertices can be either inside the isosurface or outisde, there are \(2^{8} = 256\) possible combinations of vertices. Luckily (again!) only \(14\) of those are actually relevant, since all the other are just rotations or mirrorings of these “base” cases.
Cave Generation
Starting slow
Before going 3D, I thought starting with a 2D cave generator would have been a good idea to first learn the basics of Unity. That’s when I encountered this great video series, which helped me learn a lot.
First steps into Unity
The first thing I got to work was generating a 2D map, made of squares which are randomlz chosen to be black or white (Figure 2).

As you maybe already noticed, this set-up really looks like the starting point of a Conway’s Game of Life game. Indeed, the procedural map generation will be based on cellular automation, but not on the set of rules Conway had defined.
The map generation is based on a seed system, and I also added some variables to play with for the map generation, such as a fillPercent field, with whom I could easily manage how much i wanted the map to be filled.
The rule I’ve used are failry simple:
- If the cell as more then 4 alive neighbour cells, make it alive;
- If it has less than 4 alive neighbour cells, make it die;
- If it has exactly 4 alive neighbours, let it be as it is;
This precise rule is what I found working the best to generate a cave-resembling shape. Moreover, I’ve added some tweaks to the code to make sure that near walls more cells become alive, and ensure that the more we go towards the end of the cave, the thicker the walls are. I decided to apply the rule for 5 iterations, which seemed to work just fine. Some results can be obvserved below.

In the end I played around with grid dimension, seeds, number of iterations and also tried changing the rule threshold (which was previously 4), but I didn’t get any result worth mentioning.